Bei diesem Artikel geht es darum, zu prüfen, ob sich die gewonnenen Einsichten auch auf ein ähnliches Spielsystem übertragen lassen.

Die in Abbildung 1 gezeigten Würfel kommen in einem Spiel vor. Am Ende eines Wurfs haben SpielerInnen (hier spielt der Einfachheit halber Max) 6 Würfel vor sich liegen, von denen jeder theoretisch eine andere Augenzahl und eine andere Farbe haben können.

Abb. 1: Alle möglichen Würfel eines fiktiven Spiels

Die Farben der Würfel sind: Rot, Grün, Blau, Gelb, Türkis und Magenta. Die Augenzahlen reichen jeweils von 1 bis 6.

Gewinnkombinationsprüfung
Es soll jetzt, nachdem Max mit Würfeln fertig ist, der Wurf auf bestimmte Gewinnkombinationen („GK“) hin untersucht werden:

1. Paar: 2 Würfel gleicher Farbe und gleicher Augenzahl (z.B. 2 rote Vieren)
2. 2 Paare: siehe Paar, aber 2 mal
3. 3 Paare: siehe Paar, aber 3 mal
4. Dreier: 3 Würfel gleicher Farbe und gleicher Augenzahl (z.B. 3 rote Vieren)
5. 2 Dreier: siehe Dreier, aber 2 mal
6. Vierer: 4 Würfel gleicher Farbe und gleicher Augenzahl (z.B. 4 rote Vieren)
7. Fünfer: 5 Würfel gleicher Farbe und gleicher Augenzahl (z.B. 5 rote Vieren)
8. Sechser: 6 Würfel gleicher Farbe und gleicher Augenzahl (z.B. 6 rote Vieren)
9. Zahlen 1 bis 6, alle Würfel zeigen unterschiedliche Farben
10. Zahlen 1 bis 6, alle Würfel zeigen die gleiche Farbe

Die Wertigkeit der jeweiligen GK nimmt nach unten stetig zu, also ein Sechser ist mehr wert als ein Paar.

Anders als in dem o.g. Artikel geht es also nicht nur um einen in die Prüfung einzubeziehenden Aspekt oder Faktor (Augenzahl), sondern zusammen mit der Würfelfarbe um zwei Faktoren. Daher gehe ich davon aus, dass ich für jeden untersuchten Wurf zwei Werte erhalte, nämlich die Anzahl der Augenzahlübereinstimmungen („AÜ“) und die Anzahl der Farbübereinstimmungen („FÜ“).

Beispiel-Tabellen
Um überhaupt eine Vorstellung zu bekommen, ob sich die Vorgehensweise bei der GK-Prüfung aus dem o.g. Artikel hier ebenfalls anwenden lässt, habe ich einige Tabellen aufgestellt, mit unterschiedlichen Wurfergebnissen gefüllt und per Hand die Treffer (engl. matches) abgezählt.
Jeder Würfel des Wurfs ist einmal horizontal und einmal vertikal in dieser Tabelle notiert. Beim Abzählen der Übereinstimmungen trage ich im Feld, in dem sich Zeile und Spalte schneiden, jeweils ein, wie das Ergebnis der Prüfung ausgefallen ist.
Felder in diesen Tabellen, die mit „X“ gekennzeichnet sind, entfallen bei der Überprüfung. Ein „-“ bedeutet: Keine FÜ und auch keine AÜ. „F“ wird eingetragen, wenn eine FÜ bei den beiden miteinander verglichenen Würfel vorliegt, und ein „A“, wenn eine AÜ vorliegt.

GK 9 – Der „Regenbogenwurf“
In Abb. 2 ist der von mir so genannte „Regenbogenwurf“ zu sehen, bei dem alle Farben und alle Augenzahlen genau einmal vorkommen. Dies würde GK 9 meiner obigen Liste entsprechen.
FÜ und AÜ betragen in diesem Fall beide 0.

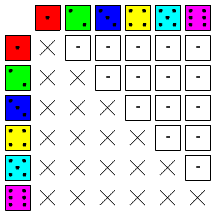
Abb. 2: „Regenbogenwurf“ — FÜ = 0; AÜ = 0

Meine Annahme ist, dass ich davon ausgehen kann, dass FÜ = 0 und AÜ = 0 immer bedeutet, dass GK 9 vorliegt. Aber schauen wir mal weiter.

GK 10 – Der „Normalfall“
Man könnte diese GK sicher auch „Straße“ nennen, geht es doch hierbei darum, alle Zahlen einer Farbe zu erwürfeln.

Abb. 2a: „Normalfall“ — FÜ = 15; AÜ = 0

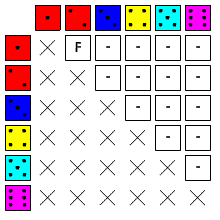
Hier (Abb. 2b) hat Max es mit einer einzigen AÜ zu tun (2 Einsen unterschiedlicher Farbe). Der Wurf ist, gemessen an der GK-Übersicht, ungünstig ausgefallen — close, but no cigar:

Abb. 2b: FÜ = 0; AÜ = 1

Hier (Abb. 2c) ist es ähnlich, nur liegt hier eine FÜ vor (2 mal rot, aber die Augenzahlen stimmen nicht überein):

Abb. 2c: FÜ = 1; AÜ = 0

Paar(e) — GK 1 bis 3
Hier (Abb. 2d) hat Max mehr Glück, denn immerhin hat er sich ein Paar erwürfelt, was laut Definition oben GK 1 darstellt und ihm ein paar Punkte bringt (kein Wortspiel):

Abb. 2d: FÜ = 1; AÜ = 1

Ich bleibe bei den Paaren und lasse Max ein wenig weiterwürfeln, bis sich zeigt, wie es um FÜ und AÜ bestellt ist, wenn zwei oder drei Paare vorliegen.
Erst einmal zwei Paare:

Abb. 2e: FÜ = 2; AÜ = 2

Und jetzt 3 Paare:

Abb. 2f: FÜ = 3; AÜ = 3

Ich stelle mir die Frage, ob es auch andere Würfe gibt, deren FÜ und AÜ so ausfallen wie bei den eben untersuchten Paar-Würfen. Obwohl ich fast sicher bin, dass die Antwort „nein“ lauten muss, fehlt mir eine Art Beweis. Es steckt allerdings zu wenig Mathematiker in mir, und ich muss mich zunächst weiter mit Vermutungen und Annahmen zufrieden geben.

Mehrling(e) — GK 4 bis 8
Um die FÜ/AÜ-Sachlage bei Würfen zu prüfen, wo es Max gelungen ist, mehrere gleiche Würfel zu erwürfeln, erstelle ich mir die folgenden Tabellen.

Und da haben wir den Salat:

Abb. 2g: Leider auch FÜ = 3; AÜ = 3

Wie anhand dieser Tabelle zu erkennen ist, habe ich mich nicht nur böse geirrt, sondern stehe mit meiner bisherigen Annahme auch noch vor einem Problem. Offenbar kann ich bei dem GK-Prüfungsergebnis FÜ = 3; AÜ = 3 nicht einfach davon ausgehen, dass hier die GK „3 Paare“ vorliegt, denn dasselbe Ergebnis kommt auch bei einem einfachen „Dreier“ (vgl. Abb. 2f) heraus.

Es sieht so aus, als bestünde dieses Problem nur in genau dem zuletzt untersuchten Fall. Aber sicher kann ich nicht sein. Daher erstelle ich noch flink die fehlenden Tabellen.
GK 5 („2 Dreier“):

Abb. 2h: FÜ = 6; AÜ = 6

Auch hier bei der GK 6 („Vierer“) gibt es Ärger:

Abb. 2i: Wie beim „Dreier“ leider auch hier FÜ = 6; AÜ = 6

GK 7 („Fünfer):

Abb. 2j: FÜ = 10; AÜ = 10

GK 8 („Sechser“):

Abb. 2k: FÜ = 15; AÜ = 15

Lösungsansatz
Ich sollte bei der GK-Prüfung noch jeweils notieren, welche der Einzelprüfungsergebnisse zusammenhängen. Stoße ich also bei einem Würfelvergleich auf eine Farb- und Augenzahlübereinstimmung („FuAÜ“), lege ich diese Würfel in einen Topf, den ich gedanklich mit „Möglicher Anwärter auf GK“ beschrifte.
Finde ich die nächste FuAÜ, würde ich die zwei an dem Vergleich beteiligten Würfel wieder in einen Topf legen. Wenn sich Augenzahl und Farbe der aktuellen Würfel mit den Würfeln gleichen, die bereits in einem Topf liegen, werden die aktuellen Würfel nicht in einen neuen Topf, sondern eben den bereits existierenden gelegt.
Das alles erinnert mich stark an meine Gedanken vom letzten Mal, als ich mich mit Gewinnkombinationsprüfung beschäftigt habe. Ob ich farblich und von der Augenzahl her zusammenpassende Würfel in einen Topf oder eine Gruppe packe, ist ja egal. Im Unterschied zu meinen damaligen Überlegungen ergänze ich heute das Modell um den Schritt, am Ende der Topf/Gruppen-Zuordnung alle Töpfe/Gruppen zu verwerfen, die nur ein Element (einen Würfel) enthalten. Was übrig bleibt, sind die Töpfe/Gruppen, die GK darstellen.

Das alles gilt, wohl gemerkt, nur für GK 1 bis 8. GK 9 („Regenbogenwurf“) müsste ich im Vorwege bereits überprüft haben, denn dort geht es ja gerade darum, 6 Töpfe mit nur einem Würfel darin zu haben.

(Schnellere?) Variante
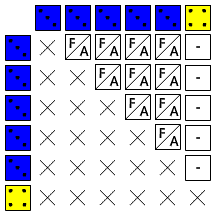
Gerade fällt mir auf, dass ich vielleicht auch schneller als Ziel kommen kann. In Abb. 3 ist Max‘ letzter Wurf zu sehen — für mich sofort als ein „Vierer“ zu erkennen. Für Flash erstmal nur Böhmische Dörfer. Das soll sich ändern.

Abb. 3: Nummerierte Würfel

Mein Plan ist es, jeden der sechs Würfel nacheinander daraufhin prüfen zu lassen, ob es bereits einen Topf gibt, der genau den gleichen Würfel (also einen Würfel gleicher Farbe und gleicher Augenzahl). Wenn ja, kommt der aktuelle Würfel mit in den Topf. Wenn nicht, lege ich ihn in einen eigenen Topf.
Das macht genau 6 Prüfungen, was sehr viel weniger ist, als ich oben noch angenommen hatte durchführen lassen zu müssen (15 Prüfungen).

Ablaufschema:
1) Gibt es bereits einen Topf für blaue Dreien?
Nein.
Hole einen neuen Topf für blaue Dreien.
Anzahl Töpfe: 1 (Topf/Elementanzahl: Topf1/1)

2) Gibt es bereits einen Topf für grüne Einsen?
Nein.
Hole einen neuen Topf für grüne Einsen.
Anzahl Töpfe: 2 (Topf/Elementanzahl: Topf1/1; Topf2/1)

3) Gibt es bereits einen Topf für blaue Dreien?
Ja!
Lege diesen Würfel in den Topf für blaue Dreien.
Anzahl Töpfe: 2 (Topf/Elementanzahl: Topf1/2; Topf2/1)

4) Gibt es bereits einen Topf für blaue Dreien?
Ja!
Lege diesen Würfel in den Topf für blaue Dreien.
Anzahl Töpfe: 2 (Topf/Elementanzahl: Topf1/3; Topf2/1)

5) Gibt es bereits einen Topf für gelbe Vieren?
Nein.
Lege diesen Würfel in den Topf für gelbe Vieren.
Anzahl Töpfe: 3 (Topf/Elementanzahl: Topf1/3; Topf2/1; Topf3/1)

6) Gibt es bereits einen Topf für blaue Dreien?
Ja!
Lege diesen Würfel in den Topf für blaue Dreien.
Anzahl Töpfe: 3 (Topf/Elementanzahl: Topf1/4; Topf2/1; Topf3/1)

Anhand der Anzahl der Töpfe würde ich sofort nach dieser Prozedur feststellen, ob die GK 9 vorliegt, bei der die Anzahl der Töpfe 6 sein muss. Das ist hier nicht der Fall. Durch diese Feststellung kann ich alle Töpfe des eben erhaltenen Ergebnisses verwerfen, die nur ein Element enthalten. [Hier habe ich mich geirrt, wie mir durch einen Einwand meines Kollegen Lars klar geworden ist.]

Was übrig bleibt, ist ein Topf mit drei Elementen, sprich: ein „Dreier“.
„Paare“, „Vierer“, „Fünfer“ und „Sechser“ kann ich ebenso leicht voneinander unterscheiden. Und auch Mischungen mehrerer GK in einem Wurf sollten damit erfasst werden können.

Allmählich wird mir klar, dass es keine allgemein gültige Vorgehensweise zur GK-Prüfung geben kann, wenn sich von Spiel zu Spiel die Parameter und GK ändern. Aber einen großen Teil der Möglichkeiten decke ich mit dem oben geschilderten Verfahren sicher ab.